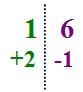Mathématiques

Les propriétés du nombre 9 sont nombreuses et étonnantes. Nous allons en voir ici un exemple. Après l'exposé de la méthode traditionnelle, une optimisation est présentée. Cette optimisation fonctionne dans toutes les divisions par 9. Elle est présentée ici à un niveau élémentaire mais elle sera développée dans d'autres sections (voir menu à gauche).

A droite de cet article, vous disposez d'un accès à un atelier d'entraînement qui va vous permettre de mieux comprendre comment fonctionne cette optimisation. Vous pourrez la lancer dès que vous serez sûrs d'avoir bien compris comment elle fonctionne.

Une vidéo commentée se trouve en dessous du lien vers l'atelier. N'hésitez pas à la lancer et à agrandir l'image.

Méthode traditionnelle

Technique :

1°) comme 5 est plus petit que 9, on est obligé de prendre 51 et de se demander : dans 51, combien de fois 9 ? Il y va 5 fois, ce qui donne 45, que l'on soustrait à gauche : il reste 6.

2°) On descend le 0 et on cherche combien de fois 9 on peut placer dans 60 ? Il y va 6 fois, ce qui donne 54, que l'on retranche à 60 : il reste 6.

3°) On descend le 1 et, dans 61, on cherche combien de fois 9. Il y va 6 fois, ce qui donne 54, que l'on retranche à 61 : il reste 7.

etc.

Optimisation

(Notez bien les couleurs utilisées, elles sont utiles dans l'explication de la technique.)

Explications

1. La manière de la poser à l'écrit

Ci-dessus, nous pouvons voir une autre façon de poser la division :

- le diviseur est à gauche (là où place le dividende d’habitude),

- le dividende est à droite (là où le diviseur est placé d’habitude),

- le quotient se trouve à la place habituelle,

- mais le reste se situe à la fin du quotient.

Cela peut sembler étrange au début, mais la pratique montre qu’il existe beaucoup d’avantages à poser une division comme ceci.

Comme dans la division traditionnelle, cette division se fait de gauche à droite.

2. La technique de calcul

(La suite de cet artcile n'est accessible qu'aux utilisateurs enregistrés.)