Un Algorithme, qu’est-ce que c’est ???

 

I – Définition

Un algorithme est en ensemble d’opérations successives réalisées en vue de résoudre un problème donné.

 

II - Exemple non mathématique

Pensez à quelqu’un qui se lève le matin et qui doit partir travailler plus tard. Il va devoir, au minimum :

 

1 – Se réveiller

2 – Enlever son pyjama

3 – S’habiller

 

Ces trois « opérations » constituent un algorithme : elles permettent de passer d’une situation de départ (le réveil) à une situation d’arrivée (le départ au travail). Le fait qu'elles soient répétées tous les jours permet de pouvoir les exécuter sans trop y réfléchir, dans le noir, ou même quand on n’est pas bien réveillé du tout :-)

 

Plus sérieusement, les algorithmes font partie intégrante de notre fonctionnement psychologique. Par exemple, quand nous avons appris à écrire et à lire, nous sommes passés par quatre phases :

 

1 – Au départ, nous ne savions pas que nous ne savions pas écrire (et lire).

 

2 – Ensuite, nous avons commencé à écrire et avons découvert, au moins au début, que nous savions que nous ne savions pas écrire (ni lire).

 

3 – A force d’entrainement, à force de faire attention à la hauteur de nos boucles, la hauteur des barres verticales des « t », des « bé, etc., il est arrivé un moment où nous nous sommes rendus compte que nous savions que nous savions écrire (et lire), mais que cela nous demandait un effort conscient.

 

4 – Maintenant, nous savons écrire de manière machinale, ce qui nous permet d’écrire vite, et nous laisse du temps pour penser à corriger certaines fotes (euh, pardon, fautes :-) ).

 

Cet algorithme de l’apprentissage est résumé sur la figure suivante :

 

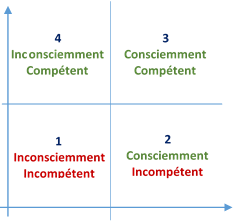
 Ces quatre phases sont quasiment omniprésentes dans tous nos apprentissages, quels qu’ils soient !

 

Elles constituent un excellent moyen de savoir où nous en sommes dans notre apprentissage.

La phase 2 est généralement la plus difficile à vivre, car elle correspond à la période où nous faisons beaucoup d'erreurs, et où il faut nous corriger. Mais c’est la phase d’apprentissage primordiale qui fera, si nous tenons bon, que les phases 3 et 4 verront le jour.

 

III - Exemples mathématiques

a)     A l’école primaire

On nous a appris à effectuer des opérations de base comme l’addition, la soustraction, la multiplication et la division.

Toutes ces opérations ont en commun qu’elles reposent chacune sur un algorithme particulier, permettant de trouver le résultat en fonction des deux nombres donnés au départ, et de l’opération qui les relie.

 

Algorithme de l’addition :

On nous a appris à commencer par additionner les chiffres des unités d’abord,

puis à additionner les chiffres des dizaines,

puis ceux des centaines, etc.,

en tenant compte des éventuelles retenues à chaque étape.

 

b)    En classes de 5^ème et de 4^ème

On nous a montré ce que sont des programmes de calculs.

Par exemple, si on lit A = x + 5, cela signifie que :

On prend un nombre x

On lui additionne 5

Et on trouve un résultat appelé A.

 

Là encore, A = x + 5 décrit un algorithme et il vaut mieux voir A = x + 5 comme l’algorithme décrit au-dessus, plutôt que de le lire « bêtement » : « A égal x plus 5 ».

 

En fait, l’école, le collège, le lycée et les établissements scolaires supérieurs (Université, Classes Préparatoire, etc.) n’existent que pour nous apprendre de nouveaux algorithmes, dans des domaines souvent très différents. Et a priori, si l’on est capable d’apprendre un algorithme dans un domaine (et de s’en souvenir), on est/sera sûrement capable d’en apprendre d’autres dans pleins de domaines différents. Il n’y a pas de limite à ce genre d’apprentissage, à part le temps dont on dispose, et/ou nos priorités.

 

Parfois, on nous fait apprendre des algorithmes, puis, plus tard, nous découvrons qu’il y avait peut-être des algorithmes bien meilleurs que ceux que nous avons appris : Par exemple, au lieu de poser l’opération 23 x 27 comme on a tous appris à le faire dès l’école primaire, il existe un algorithme (multiplication 23 x 27) permettant d’en trouver mentalement le résultat en moins de 5 secondes.

Changer d’algorithme est alors une affaire de choix, ou de nécessité.

 

IV – Comment reconnaitre un algorithme ?

 

a)     Parfois, les algorithmes portent des noms

i) En calcul :

L’addition, la soustraction, la multiplication ou la division sont des noms donnés à des algorithmes biens définis.

La distributivité, apprise en 5^ème et 4^ème en est un autre.

Les produits remarquables (programme de 3^ème) en sont aussi.

Etc.

 

ii) En géométrie :

Le théorème de Pythagore en est un.

Le théorème de Thalès un autre.

La trigonométrie (cosinus, sinus et tangente) qui sont au programme en 3^ème en est un également, et il permet, comme le théorème de Pythagore et celui de Thalès, de passer d’un problème de géométrie à un problème de calculs.

Etc.

 

b)    Parfois, ils ne portent pas de noms

Il appartient alors à chaque élève d’en avoir une bonne image en mémoire, et de savoir ce qu’il permet de faire.

Par exemple, l’algorithme présenté sous la forme (aⁿ)^m = a^nxm permet, dès qu’on rencontre un calcul ressemblant à (aⁿ)^m de l’écrire sous la forme a^nxm, et inversement.

On pourrait aussi prendre l’addition entre deux fractions, ou les enchaînements d’opérations.

 

La mémoire, et l’entraînement, sont alors très utiles, même si, parfois, ces algorithmes peuvent être « retrouvés » à partir de quelques propriétés élémentaires.

 

V – Des algorithmes, pour quoi faire ?

 

En y réfléchissant un peu, on se rend compte que tout ce que nous faisons repose souvent sur un ou plusieurs algorithmes.

Leur raison d’exister est principalement une question d’économie de temps  et d’énergie : quelqu’un qui aurait à additionner quinze mille fois le nombre 2 aura plus vite fait de calculer 15 000 x 2. L’algorithme de l’addition peut parfois être avantageusement remplacé par celui de la multiplication :-).

 

Mais comme on n’a rien sans rien, si l’on veut s’économiser du temps pour certaines tâches, il faut en « perdre » un peu en apprenant certains algorithmes.

 

En mathématiques, et en Sciences en général, on est souvent amené à rencontrer des calculs qui se ressemblent. Les algorithmes jouent alors à plein régime, permettant ainsi de gagner du temps.

 

En Informatique (en programmation), les programmes ne sont en fait que des algorithmes traduits dans un langage que les ordinateurs savent interpréter.

 

Quand on veut passer des examens ou des concours, les algorithmes sont souvent d’une aide inestimable, et permettent des gains de temps précieux, surtout quand le concours ou l’examen se déroule en temps limité.

 

C’est à chacun d’entre nous de maîtriser les algorithmes qui lui seront utiles par la suite, ou qui pourront l’être.