Le Duplex d'un nombre

Dans cet article, lorsque deux chiffres seront placés comme ceci 23 le petit chiffre (le 2) de gauche sera une retenue qui sera ajoutée au chiffre situé à sa gauche.

1ère Partie - Le Duplex d'un nombre, qu'est-ce que c'est ?

Définition :

Pour un chiffre, par exemple le nombre "a" ne possède qu'un seul chiffre (le chiffre "a"), son Duplex est égal au carré de son chiffre, c'est à dire à "a" multiplié par lui-même.

On notera D(a) = a² .

Exemple : Pour le nombre "7", D(7) = 7² = 49.

Pour un groupe de deux chiffres, par exemple le groupe "ab" (où a et b représentent chacun un seul chiffre), son Duplex est égal au double produitdes chiffres qui le composent .

On aura donc D(ab) = 2 x a x b = 2ab .

Exemple : Pour le nombre "43", D(43) = 2 x 4 x 3 = 24. 

Pour un groupe de trois chiffres, noté par exemple "abc", nous aurons : 

D(abc) = 2ac + b² .

Exemple : Pour le groupe  "245", nous aurons D(245) = 2 x 2 x 5 + 4² = 20 + 16 = 36. 

Pour un group de quatre chiffres, noté "abcd", nous aurons

D(abcd) = 2ad + 2bc ou  encore 2(ad + bc) ce qui sera souvent plus rapide à calculer .

Exemple : Pour le groupe "1234", nous aurons D(1234) = 2 x 1 x 4 + 2 x 2 x 3 = 8 + 12 = 20.

 Ces quelques exemples montrent une certaine récurrence dans la méthode, récurrence que nous pouvons illustrer comme ceci :

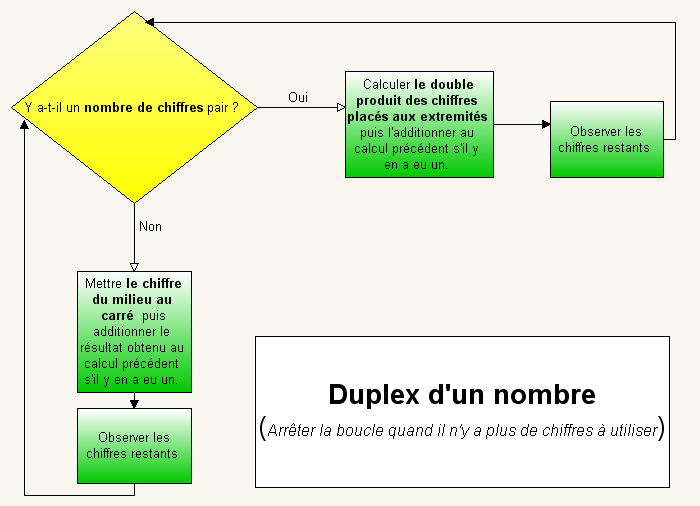
2ème Partie - A quoi peut bien servir le Duplex d'un nombre ?

(Dans toute la suite de cette section, pour les nombres à deux chiffres et plus,

nous utilisons les Duplex de gauche à droite. La méthode serait la même en les utilisant de droite à gauche.)

La méthode du Duplex exposée ci-dessus permet de calculer le carré d'un nombre entier rapidement, et ce quel que soit le nombre de chiffres qu'il possède.

Pour cela, il suffit de savoir que :

La suite de cet article n'est accessible qu'aux utilisateurs enregistrés.