Racine carrée (part.1) - A partir d'un carré parfait

En 4ème, il est nécessaire de savoir ce qu'est une racine carrée, et de savoir calculer la racine carrée d'un nombre. D'ordinaire, cette dernière activité est faite à la calculatrice pour les nombre à trois ou quatre chiffres. Cependant, il existe plusieurs  moyens de calculer la racine carrée d'un nombre. Les méthodes présentées ici sont basées sur le Duplex d'un nombre. Elles présentent l'intérêt d'être explicables par le calcul littéral qui sera développé plus tard en 4ème, puis en 3ème.

Dans tout ce qui suit :

• Le caractère "/" symbolisera une séparation entre deux groupes de chiffres dans un nombre.
• Nous ne chercherons que les racines carrées des carrés parfaits.
• Les couleurs utilisées pour écrire les nombres sont importantes. Le rouge est réservée aux racines carrées, le bleu aux carré, et le violet aux retenues venant du duplex du milieu.

Partie 1 - Définition d'une racine carrée, exemples simples, notation et lecture.

Exemple 1 : On sait que 3 x 3 = 3² = 9 .  

Dans la section sur le carré d'un nombre, on a vu que 9, 3² et 3 x 3 sont appelés "les carrés de 3".

On dit aussi que "la racine carrée de 9 est égale à 3 " (ou bien que "9 a pour racine carrée 3 ").

A l'écrit, il existe une notation équivalente à cette dernière phrase : 

Dans cette notation, il est très important que la barre horizontale de l'espèce de "v" recouvre complètement le nombre placé en dessous de lui.

Si ce nombre avait trois chiffres, cette barre horizontale les recouvrerait tous les trois : 

Il ne faudrait pas écrire ce qui suit : 

 puisque la barre horizontale du symbole "racine carrée" ne recouvre pas tout le nombre 225.

 Exercice de lecture - Lire à haute voix les égalités suivantes :

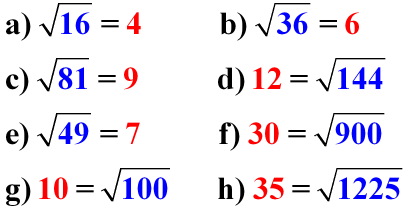
Partie 2 - Calcul de la racine carrée d'un carré parfait

Ce qu'il faut avoir en tête : 

• Le Duplex d'un nombre à un chiffre est son carré : D(a) = a².
• Le Duplex d'un nombre à deux chiffres est le double produit de ses deux chiffres : D(ab) = 2 x a x b.
• Le carré d'un nombre est égal à la "somme" de tous les duplex qu'on peut créer à partir de ses chiffres :
  
• 
  

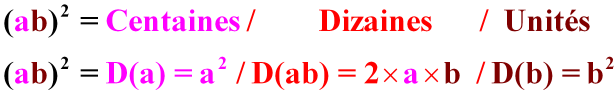
Méthode n°1 - Utilisation du dernier chiffre

Exemple : Imaginons que l'on désire calculer 

L'observation du chiffre des unités, le 9, nous indique que la racine carrée de 169 devait se terminer soit par 3 (parce que 3 x 3 = 9) ou par 7 (car 7 x 7 = 49).

Par ailleurs, le nombre 169 possède trois chiffres, donc il est le carré d'un nombre à deux chiffres (voir le Duplex). Nous savons donc que 169 a été obtenu par (a3)² ou bien par (a7)². 

Maintenant, il nous faut décomposer 169 en groupes de deux chiffres en partant du chiffre des unités.

Nous avons donc 169 = 01/69.

Le 1er groupe, 01, va nous servir à trouver le nombre a en nous posant la question suivante :

"Quelle doit être la valeur maximale de a pour que a x a s'approche le plus possible de 01 ?"

La réponse est immédiate : a = 1.

Donc nous savons maintenant que 169 a été obtenu soit avec (13)², soit avec (17)².

Il ne reste plus qu'à tester ces deux nombres :

(17)² = D(1)/D(17)/D(7) = 1/₁4/₄9 = 289 donc 17 ne convient pas.

mais (13)² = D(1)/D(13)/D(3) = 1/6/9 = 169 !

Avantage(s) de cette méthode : 

• Les calculs pour déterminer le chiffre des unités puis le chiffre des dizaines sont simples.

Inconvénient(s) de cette méthode : 

• Il est possible que nous ayons plusieurs réponses possibles (comme 13 et 17) que nous devions tester à la fin. C'est contraignant, peu productif et nous oblige à effectuer des calculs "complexes" avec les duplex.

Méthode n°2

Nous allons optimiser la méthode n°1en faisant un test beaucoup plus tôt.

La suite de cet article n'est accessible qu'aux utilisateurs enregistrés.