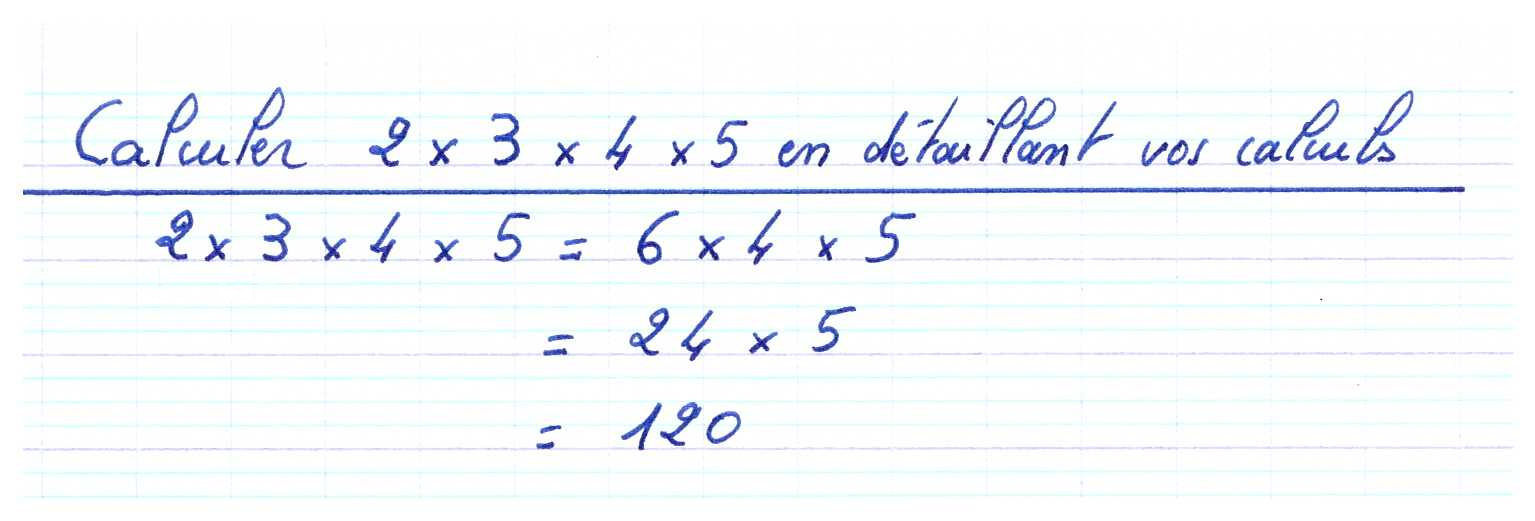Enchaînements d'opérations

L'enchaînement d'opérations fait référence à toutes les manières possibles de combiner les nombres et les quatre opérations de base que sont l'addition, la soustraction, la multiplication et la division, à l'ordre dans lequel les effectuer et à la présentation écrite des calculs effectués.

Cela marque donc la fin des opérations posées et les débuts des calculs en lignes, comme expliqués dans la 1ère partie.

C'est aussi la fin d'une époque : à partir de l'année de 5ème, en mathématiques, les élèves doivent apprendre à changer leurs habitudes.

Alors qu'ils ont appris à tenir compte des nombres dans les calculs, on va maintenant leur demander d'observer les signes des opérations afin de savoir comment ils doivent organiser leurs calculs (lequel effectuer en premier, lequel faire ensuite, etc.).

Cela va leur demander beaucoup d'attention, et provoquer de fréquentes erreurs jusqu'à ce que certains automatismes soient mis en place.

La patience et l'obstination sont de rigueur...

1ère partie - Quelques explications préliminaires...

a) La fin des opérations posées.

A partir de l'année de 5ème, la manière de présenter les calculs et les explications est profondément modifiée par rapport aux enseignements de l'école élémentaire, ou même par rapport à l'enseignement de 6ème.

Cela s'explique par le fait que les élèves de collège ont pour charge d'apprendre, entre le niveau 5ème et celui de 3ème, à rédiger des démonstrations qui peuvent contenir des explications (phrases) et des calculs.

Par exemple :

Là où un élève de 6ème écrira :

 356

+ 59

 415

Les achats ont coûté 415€.

Un élève de 5ème devra écrire :

356 € + 59 € = 415 €

Les achats ont coûté 415€.

Cette manière de présenter calculs et explications sous-entend donc plusieurs choses :

• - Plus aucun calcul ne doit être posé sur une feuille d'examen (sauf pour le calcul littéral, mais nous verrons cela plus tard :-) ).
• - Les calculs sont effectués mentalement, ou bien posés au brouillon, ou bien sur une calculatrice.
• - Les calculs doivent apparaître avant leur explication.
• - Les unités (dans l'exemple, les €) peuvent apparaître dans les calculs. Elles en font même partie intégrante et il est fortement recommandé de les écrire (ne serait-ce que pour garder en tête ce que l'on est en train de calculer).

 

b) Le signe "=" a-t-il une signification ou bien n'est-il présent que pour faire joli ?

En mathématiques, tous les symboles ont une signification particulière. Le signe "=" ne fait pas exception à cette règle.

Le signe "=" signifie que le résultat écrit à sa droite

est l'équivalent de l'ensemble des calculs situés à sa gauche.

Par exemples :

• - Quand on écrit 2 × 3 = 6, cela signifie que 6 est l'équivalent du produit de 2 par 3.
• - Quand on écrit 2 × 3 - 1 = 5, cela signifie que 5 est l'équivalent de la différence entre le produit de 2 par 3 et 1.
• 
  

La conséquence de ce qui précède est donc que :

Le signe "=" ne doit être suivi que du résultat final

ou bien d'une expression équivalente au résultat final.

Par exemples :

Si on a le calcul 6 + 2 + 3 à effectuer, nous pourrons écrire :

6 + 2 + 3 = 11

ou bien

6 + 2 + 3 = 8 + 3 = 11

ou bien

6 + 2 + 3 = 6 + 3 + 2 = 9 + 2 = 11

Si on a le calcul 2 + 3 + 4 + 7 à effectuer, nous pourrons écrire :

2 + 3 + 4 + 7 = 16

ou bien

2 + 3 + 4 + 7 = 5 + 11 = 16

etc.

Par contre, dans ce dernier exemple, si nous écrivons :

2 + 3 + 4 + 7 = 5 + 4 = 9 + 7 = 16

nous serons sûrement sanctionnés (perte de points dans un contrôle par exemple) car les différents signes "=" qui se trouvent dans ce calcul n'ont pas le sens qu'ils devraient avoir :

• - En effet, écrire que 2 + 3 + 4 + 7 = 5 + 4 n'a pas de sens car le + 7 a été oublié dans les calculs placés à droite du "=".
• - De même, écrire que 5 + 4 = 9 + 7 n'a pas de sens (car 5 + 4 = 9 et pas à 9 + 7 !).

Munis de ces précieux renseignements, nous allons voir comment organiser nos calculs dans les cas où plusieurs opérations identiques ou différentes s'enchainent dans un calcul.

2ème partie - Enchaînements d'opérations identiques

Règle à suivre :

. Quand il y a des opérations identiques dans tous le calcul,

il suffit de commencer par l'opération qu'on lit en début de ligne.

(On peut éventuellement effectuer tous les calculs d'un seul coup si les nombres ne sont pas trop compliqués).

Exemples :

1) Si on veut calculer 2 + 3 + 4 + 7,

il est possible de calculer mentalement d'abord 2+3 qui donne 5, puis d'ajouter 4 qui donne 9, puis d'ajouter 7. On trouve 16 et on écrit alors sur la feuille :

2 + 3 + 4 + 7 = 16.

2) Si on veut calculer 356 + 42 + 98,

il peut être un peu plus risqué de tout calculer d'un seul coup.

Donc nous allons décomposer ce calcul selon la règle disant qu'on effectue la 1ère opération lue, c'est à dire 356 + 42 (qu'on peut poser au brouillon).

Cela donne 398. Nous écrivons alors sur la feuille :

356 + 42 + 98 = 398 + 98

Puis nous effectuons 398 + 98 qui donne 496.

Nous écrivons alors ce résultat final sur la feuille, en dessous de la ligne précédente :

356 + 42 + 98 = 398 + 98

        = 496.

(remarquez bien les deux signes "=" placés l'un sous l'autre)

 

[Il est toléré d'écrire 356 + 42 + 98 = 398 + 98 = 496 mais il vaut mieux éviter car cela rend les calculs difficiles à lire et à vérifier s'il y a plus de quatre opérations à la suite.]

 

Une bonne règle à appliquer systématiquement est d'avoir un seul signe "=" par ligne écrite.

Jamais plusieurs signes "=" sur la même ligne !

 

3) Si on veut calculer 2 × 3 × 4 × 5, on peut calculer mentalement 2 × 3 qui donne 6, puis multiplier ce résultat par 4 qui donne 24, puis multiplier ce résultat par 5 qui donne...120.

Nous écrirons alors simplement sur la feuille :

2 × 3 × 4 × 5 = 120.

Avec les multiplications, cela devient vite compliqué.

Dans le cas précédent, il vaut mieux décomposer de la manière suivante :

On part de 2 × 3 × 4 × 5.

On calcule d'abord 2 × 3 qui donne 6.

On écrit alors sur la feuille :

2 × 3 × 4 × 5 = 6 × 4 × 5

Puis on effectue 6 × 4 qui donne 24.

On écrit alors sur notre feuille, en dessous de la ligne précédente :

2 × 3 × 4 × 5 = 6 × 4 × 5

      = 24 × 5

Puis on effectue 24 × 5 qui donne 120.

On écrit ce résultat sur notre feuille, en dessous de la ligne écrite précédemment.

Voici donc ce qui doit appraitre sur la feuille de l'élève qui a respecté toutes les règles et toutes les étapes décrites ci-dessus :

 

Quand il sera demandé de "détailler les calculs" (comme sur notre illustration), il faudra :

- Effectuer les opérations une par une (on pourra en faire plusieurs d'un seul coup si les nombres ne sont pas trop compliqués),

- Changer de ligne à chaque fois qu'on veut mettre un "=",

- Penser à recopier tous les nombres et toutes les opérations qui n'ont pas été utilisés, en gardant leur positions intactes (il faut éviter de changer des nombres (ou des opérations) de place !)

 

On doit garder à l'esprit que ce qui apparaît sur la feuille doit illustrer exactement la méthode suivie pour réaliser toutes les opérations présentes dans le calcul donné au départ (c'est par ailleurs un excellent moyen d'indiquer à un élève qui se trompe l'endroit exact où il a fait une erreur).

 

4) On veut calculer 6 + 4 - 5

Il peut sembler étrange que dans cette section réservée à une suite d'opérations identiques, nous trouvions un exemple dans lequel figurent une addition et une soustraction.

En fait, bien qu'étant deux opérations aux fonctionnement différents, l'addition et la soustraction sont considérées comme étant dans la même catégorie et, à ce titre, elles entrent dans cette section.

Par conséquent, la première opération qui doit être effectuée est la première qui est lue dans la ligne de calcul, c'est à dire 6 + 4 qui donne 10.

Nous écrirons donc :

6 + 4 - 5 = 10 - 5

    = 5

3ème partie - Enchaînements d'opérations différentes

Règle à suivre :

. Il faut effectuer les multiplications et les divisions

avant de passer aux additions et aux soustractions.

En clair, si des opérations différentes sont présentes dans un calcul, voici comment cela se déroulera :

- D'abord, nous effecturons les multiplications et les divisions (soit toutes en même temps, soit les unes après les autres).

- Ensuite, il ne restera que des additions et des soustractions. Nous effecturons alors l'opération placée en début de ligne.

Exemples :

1) On veut calculer 3 + 7 × 6.

La présence du signe "×" indique que nous devons effectuer le produit avant de l'ajouter à 3.

Nous écrirons donc sur notre feuille :

3 + 7 x 6 = 3 + 42   (remarquez comme le 3 est resté à sa place)

     = 45

2) On veut calculer 2 × 4 + 7 × 6

La présence des deux signes "×" indique que nous devons commencer par ces deux multiplications avant d'additionner leurs résultats ensemble.

Comme 2 × 4 donne 8 et 7 × 6 donne 42, nous écrirons :

2 × 4 + 7 × 6 = 8 + 42

       = 50

 3) On veut calculer 4 + 7 × 6 - 12 ÷ 4

 Nous constatons la présence des signes " × " et " ÷ ". Nous devons donc effectuer d'abord 7 × 6 et 12 ÷ 4.

 Comme 7 × 6 donne 42 et 12 ÷ 4 donne  3 , nous écrirons :

 4 + 7 × 6 - 12 ÷ 4 = 4 + 42 - 3

          = 46 - 3

          = 43

Dans cet exemple, nous aurions pu d'abord effectuer la multiplication sans toucher tout de suite à la division. Cela aurait donné :

4 + 7 × 6 - 12 ÷ 4  = 4 + 42 - 12 ÷ 4

         = 4 + 42 - 3

         = 46 - 3

         = 43

[ Et, si nous avions décidé de ne pas passer à la ligne à chaque fois que nous effectuons un calcul, voici ce que cela donnerait :

4 + 7 × 6 - 12 ÷ 4 = 4 + 42 - 12 ÷ 4 = 4 + 42 - 3 = 46 - 3 = 43

On peut constater que la lecture de ce calcul n'est pas très facile, et que cela ne facilite pas sa vérification.

C'est pour cette raison que cette manière de présenter une suite de calculs n'est généralement pas acceptée (et peut être sanctionnée lors de certains examens comme le Brevet des Collèges). ] 

 

4ème partie - Calculs avec parenthèses et crochets

Dans certains cas, des parenthèses ou des crochets sont présents dans une ligne de calcul.

Règle à suivre : 

. Quand il y a des parenthèses (ou des crochets) dans une ligne de calculs,

nous devons en priorité effectuer les calculs qui se trouvent à l'intérieur de ces parenthèses(ou de ces crochets)

en respectant aussi les règles précédemment expliquées.

Exemples : 

1) On dont calculer 3×(2+4×5).

Nous voyons clairement les parenthèses au premier coup d'oeil. Donc nous devons effectuer en priorité les calculs qui s'y trouvent, c'est à dire 2+4×5. Et comme dans ces calculs il y a deux opérations différentes, nous devons effectuer d'abord la multiplication. Comme 4×5 donne 20, nous écrirons sur notre feuille :

3×(2+4×5) = 3×(2+20)

Des parenthèses étant toujours présentes, nous devons maintenant effectuer 2+20 qui donne 22.

Et comme il n'y aura plus de calcul à effectuer dans les parenthèses, celles-ci disparaissent.

Nous allons donc écrire, en dessous de la ligne précédente :

3×(2+4×5) = 3×(2+20)

         = 3×22

         = 66.

2) On doit calculer (2 + 4×5) + (20 - 3×6)

Nous devons donc effectuer les calculs qui se trouvent dans les parenthèses. Mais lesquels faire en premier ?

Ici la réponse est simple : nous voyons qu'il y a des multiplications dans les deux expressions entre parenthèses.

Donc nous pouvons les faire en même temps toutes les deux : 4×5 donne 20 et 3×6 donne 18. Nous écrirons donc : 

(2 + 4×5) + (20 - 3×6) = (2 + 20) + (20 - 18)

Nous devons maintenant effectuer 2 + 20  et 20 - 18.

Là encore nous pouvons les effectuer en même temps toutes les deux. Nous écrirons donc, en dessous de la ligne précédemment écrite : 

(2 + 4×5) + (20 - 3×6) = (2 + 20) + (20 - 18)

            = 22 + 2 (les parenthèses ont encore disparu puisqu'il n'y a plus de calculs à l'intérieur)

            = 24

3) On doit calculer 2 + [4 × (7 - 2)]

Nous voyons des parenthèses à l'intérieur des crochets.

Dans ces cas-là, il faut toujours effectuer les calculs qui se trouvent dans les parenthèses (ou crochets) placées le plus à l'intérieur des autres .

Donc ici, nous devons effectuer d'abord 7 - 2 qui donne 5. Nous écrivons donc :

2 + [4 × (7 - 2)] = 2 + [4 × 5]

Maintenant nous passons au calcul dans les crochets. Le résultat est 20 et les crochets vont disparaître. Nous continuons donc à écrire : 

2 + [4 × (7 - 2)] = 2 + [4 × 5]

            = 2 + 20

            = 22.