Les noms des calculs

Dans cet article, il est recommandé de prêter attention aux couleurs utilisées dans les calculs et dans les phrases qui les décrivent pour bien comprendre comment on peut passer de l'un à l'autre.

Pour une meilleur compréhension, il est aussi recommandé de maîtriser les enchainements d'opérations.

1ère partie - Ce que nous avons tendance à faire...et ce qu'il va falloir changer

Mentalement, ou même à haute voix, nous avons appris principalement à lire un calcul de gauche à droite, ou de droite à gauche.

Par exemple, si nous avons 5 + 3 = 8, nous le lisons "cinq plus trois égal huit" ou bien "huit est égal à cinq plus trois".

Effectivement, dans la vie quotidienne, nous n'avons pas besoin d'en faire davantage : nous devons parler vite, répondre vite, écrire vite, et la manière de lire les calculs exposée ci-dessus suffit largement à nos besoins immédiats.

Mais à l'Ecole, il en est tout autrement !

Au collège, il va falloir changer nos habitudes de lecture des calculs. A partir de l'année de 5ème, les compétences attendues de la part des élèves sont :

• De prêter attention aux signes présents dans les calculs à effectuer,
• D'utiliser le vocabulaire mathématique correspondant aux calculs étudiés,
• De distinguer quelles opérations sont prioritaires,
• Et donc de savoir organiser un calcul, ou de pouvoir dire comment une suite d'opérations a été orgainisée afin de résoudre un problème.

En détails, un élève de collège doit donc apprendre à  : 

• Décrire un calcul avec une phrase,
• Comprendre un programme de calcul
• Construire un programme de calcul
• Développer, en calcul, une certaine capacité d'abstraction (grâce au calcul littéral notamment)

Tous ces apprentissages sont étalés sur les trois ans que représentent les années de 5ème, 4ème et 3ème.

La première étape a donc lieu en 5ème et elle consiste a apprendre à décrire un calcul en une phrase, description qui doit rendre compte de toutes les opérations présentes dans le calcul, et de la manière dont il serait organisé s'il était effectué en détails.

2ème partie - Les règles de base pour nommer un calcul contenant une seule opération

Rappels

Dès l'école primaire, les élèves ont appris que : 

- Une addition est aussi appelée une somme.

- Une soustraction est aussi appelée une différence.

- Une multiplication est appelée un produit.

- Une division est appelée un quotient.

Ce vocabulaire des opérations, pour être juste, n'en est pas moins incomplet.

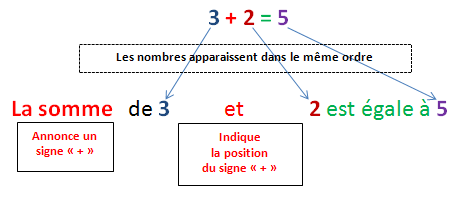
En effet, si nous écrivons "3 + 2 = 5", 5 est appelé une somme.

Mais, puisqu'il y a un signe "=" entre 3 + 2 et 5, cela signifie que 3 + 2 est aussi une somme ! 

Plus précisément, 3 + 2 (ou bien 5) est "la somme de 3 et 2".

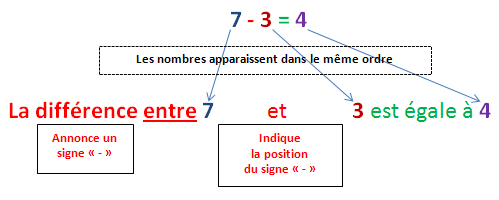
De la même manière, si nous avons "7 – 3 = 4 ", 4 sera appelé une différence, donc 7 – 3 est aussi appelé une différence.

On dit même que "7 – 3 est la différence entre7 et 3".

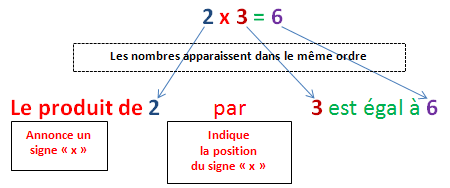
De même, avec 2 x 3 = 6 , nous dirons que 6 est un produit, tout comme 2 x 3 qui sera "le produit de 2 par 3".

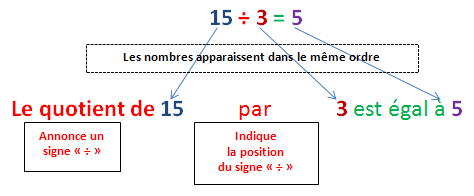
Et bien sûr, 15 ÷ 3 = 5 nous dirons que si 5 est un quotient, alors 15 ÷ 3 est aussi "le quotient de 15 par 3".

Remarques sur la construction de ces phrases

a) Pour la somme : 

On vient de voir que 3 + 2 = 5 peut se lire "la somme de 3 et 2 est égale à 5". 

En mettant en parallèle la phrase "mathématique"

3 + 2 = 5 

et la phrase littérale

"la somme de 3 et 2est égale à 5",

nous pouvons observer que : 

- le petit mot "et" se trouve à l'endroit où était le signe "+" dans le calcul,

- le mot "somme" annonce qu'il y a une addition, mais n'indique pas où elle se trouve,

- dans le calcul et la phrase, les nombres apparaissent dans le même ordre : d'abord le 3, puis le 2 et enfin le résultat 5,

- dans la phrase littérale, il n'y a pas le mot "plus", ni le mot "résultat", ni le mot "addition". Ces mots sont (et seront) exclus de ce type de phrases car il n'appartiennent pas au vocabulaire mathématique : ils appartiennent au langage quotidien qui n'a rien à voir avec le langage mathématique, dans lequel un mot ne peut avoir qu'une seule signification.

b) Pour la différence :

De même, si nous avons le calcul

7 – 3 = 4 ,

nous le lirons

"la différence entre 7 et 3 est égale à 4"

et nous pouvons faire le même genre d'observations que pour la somme : 

- le mot "différence" est toujours suivi du mot "entre"

- le mot "différence" annonce la présence d'une soustraction, mais n'indique pas la position du signe "–",

- la position du signe "– " est indiquée par la position du petit mot "et" dans la phrase,

- les nombres apparaissent dans le même ordre dans le calcul et dans la phrase : d'abord le 7, puis le 3 et enfin le 4,

- les mots "soustraction", "moins" et "résultat" sont (et seront) exclus de ce genre de phrases.

c) Pour le produit : 

Si nous avons

2 x 3 = 6 ,

nous le lirons/dirons

"le produit de 2 par 3 est égal à 6"

et, là encore, nous observons que :

- le mot "produit" annonce la présence du signe "x" mais pas sa position,

- la position du signe "x" est donnée par le mot "par" placé entre le 2 et le 3,

- les nombres apparaissent encore dans le même ordre que dans le calcul,

- les mots "multiplié par", "fois" et "résultats" sont (et seront) exclus de ces phrases.

d) Pour le quotient : 

Si nous avons

15 ÷ 3 = 5 ,

nous dirons/lirons

"le quotient de 15 par 3 est égal à 5"

et nous ferons les mêmes observations que précédemment : 

- le mot "quotient" annonce la présence du signe "÷" mais n'indique pas sa position,

- la position du signe "÷ " est donnée grâce au mot "par" placé entre 15 et 3,

- les mots "divisé par" et "résultat" sont (et seront) exclus de ces phrases.

 En images, cela donne : 

Pour la somme : 

Pour la différence : 

Pour le produit : 

Pour le quotient : 

 3ème partie - Cas des calculs avec plusieurs opérations

La suite de cet article n'est accessible qu'aux utilisateurs enregistrés.

Les règles d'écritures sont donc les suivantes : 

• On annonce les signes des opérations,
• On indique leurs positions grâce aux petits mots "et" ou "par",
• Les nombres appraissent dans le même ordre que dans le calcul.

A) Avec plusieurs fois la même opération

Exemple 1 : Nous avons 3 + 2 + 4 =9

Imaginons que nous ne connaissions pas le résultat final et que nous devions le trouver nous-mêmes.

D'après la règle de calcul adaptée, nous aurions quelque chose comme : 

A = 3 + 2 + 4

A =  5 + 4

A = 9

Grâce à l'avant dernière ligne A = 5 + 4, nous voyons que la dernière opération effectuée est la somme de 5 et 4.

Notre calcul 3 + 2 + 4 est donc une somme , et sa description aura la structure d'une phrase décrivant une somme simple :

  

La somme de ... et 4.

Nous n'avons pas le droit de parler du 5 (car il n'était pas présent dans le calcul d'origine), mais nous savons que ce 5 a été obtenu par la somme de 3 et 2.

Donc notre phrase littéral sera : 

La somme de la somme de 3 et 2 et 4.

Il ne reste maintenant qu'à placer l'équivalent du "= 9" que nous avons négligé jusqu'à présent.

3 + 2 + 4 =  9 sera donc décrit par "La somme de la somme de 3 et 2 et 4 est égale à 9".

Si nous lisons d'une traite cette phrase "La somme de la somme de 3 et 2 et 4 est égale à 9", elle semble n'avoir pas beaucoup de sens.

Il faut donc "l'aérer" avec quelques virgules. Voici une possibilité : 

"La somme de, la somme de 3 et 2, et 4, est égale à 9".

 

Exemple 2 : Nous avons 10 – 2 – 3 = 5.

Imaginons que nous ne connaissions pas le résultat final et que nous devions le trouver nous-mêmes.

D'après la règle de calcul adaptée à ce cas, nous aurions quelque chose comme :

B = 10 – 2 – 3

B =  8 – 3

B = 5

L'avant dernière ligne nous indique que nous aurions à faire la différenceentre 8 et 3 .

Notre calcul 10 – 2 – 3 est donc une différence, et sa description aura la structure d'un différence simple :  

La différence entre ... et 3.

Nous n'avons pas le droit de parler du 8 (car il n'était pas présent dans le calcul d'origine).

Par contre, nous savons que ce 8 a été obtenu par la différence entre 10 et 2.

Donc nous aurons : 

La différence entre la différence entre 10 et 2 et 3.

Notre phrase finale sera donc : 

La différence entre la différence entre 10 et 2 et 3  est égale à 5.

Là encore, il nous faut faire des pauses en la lisant. Les virgules sont nécessaires : 

La différence entre, la différence entre 10 et 2,  et 3,  est égale à 5.

Exemple 3 : Nous avons 2 x 3 x 4 = 24 .

Là encore, il faut imaginer que nous faisons nous même les calculs en suivant la règle adaptée :

C = 2 x 3 x 4

C =  6 x 4

C = 24.

Comme les cas précédents, c'est l'avant dernière ligne du calcul qui va nous donner la structure de notre phrase : 

Le produitde ... par4.

Comme le 6 venait du produit de 2 par 3, nous aurons donc comme phrase : 

Le produit du produit de 2 par 3 par 4 est égal à 24.

Ici encore, des virgules sont nécessaires : 

Le produit, du produit de 2 par 3, par4, est égal à 24 .

Exemple 4 : Nous avons 42 ÷ 2 ÷ 3 =  7

Si nous avions fait le calcul en suivant la règle adaptée, nous aurions :

D =  42 ÷ 2 ÷ 3

D =  21 ÷ 3

D =  7

L'avant dernière ligne nous est à nouveau d'une grande aide pour la structure de la phrase : 

Le quotient de .... par 3.

Comme 21 venait du quotient de 42 par 2, nous aurons donc : 

Le quotient  du quotient de 42 par 2 par 3 est égal à 7.

Avec des virgules, c'est beaucoup mieux : 

Le quotient,  du quotient de 42 par 2, par 3, est égal à 7 .

Bilan : 

Ces quelques exemples montrent :

• Qu'il est nécessaire de savoir de quoi sera constitué l'avant dernière ligne du calcul afin de déterminer la structure de la phrase,
• Qu'il y a autant de mots comme "somme", "différence", "produit" et "quotient" qu'il y avait de signes dans le calcul d'origine.
• 
  

Question : Y a-t-il des "simplifications" possible dans certaines de ces phrases ?

Réponse : Oui mais uniquement lorsqu'il n'y a que des sommes ou des produits.

Par exemple, dans 3 + 2 + 4 =  9, nous aurions pu dire/écrire aussi : La somme de 3, de 2 et de 4 est égale à 9".

Ou bien, dans  2 x 3 x 4  = 24 , nous aurions pu dire/écrire que "Le produit de 2 par 3 et par 4 est égale à 24".