Des soustractions impossibles ?
1ère partie - Quelques exemples...
A l'école élémentaire, nous avons appris, plus ou moins laborieusement, que 2 + 1 = 3 puis, un peu plus tard, que 3 - 2 = 1.
Devenue une habitude de pensée, nous n'y faisons plus du tout attention et traitons généralement ce genre de calcul par le plus grand "mépris" : "trop facile" disent les uns, "tout le monde le sait" disent les autres.
Sont arrivées ensuite les soustractions qu'il fallait poser. Et là, un obstacle s'est forcément présenté : si nous devons poser la soustraction 35 - 18, nous devons, à un moment ou un autre, nous dire :
- "dans la colonne des unités, je dois enlever 8 à 5".
Considérée comme "impossible" (car on ne peut normalement pas enlever une grande quantité à une plus petite), nous nous sommes trouvés bloqués, jusqu'à ce que le maître, ou la maîtresse, arrive et nous explique une "astuce", une "technique" pour parvenir au bout de notre calcul :
La gestion des retenues.
Ouf ! Sauvés !
Maintenant, toutes les soustractions n'ont qu'à bien se tenir !
Et finalement, grâce à la méthode des retenues, on peut effectuer toutes les soustractions n'est-ce pas ?
Ah bon ?
Vous en êtes sûrs ?
Essayez donc alors de calculer 2 - 3 pour voir !
Et oui, malheureusement, pour une"simple"soustraction comme 2 - 3, nous ne pouvons pas trouver les fameuses retenues qui nous permettent de nous en tirer.
Et nous somme bloqués à nouveau... Frustrant n'est-ce pas ?
2ème partie - Un peu de bricolage mathématique élémentaire...
Bien ! Il nous faut trouver un moyen d'effectuer 2 - 3.
Pour y arriver, nous pourrions peut-être utiliser ce que nous savons à propos de 3 :
Nous savons que 2 + 1=3 .
Donc, pour effectuer 2 -3 , nous avons 2 et nous devons lui enlever 3, c'est à dire que ... nous pouvons lui enlever 2 puis 1.
Autrement dit, nous avions 2 -3 et nous le transformons en 2 - 2 - 1.
Mais, si nous observons bien ce dernier calcul (2 - 2 - 1 ), la première opération à faire est 2 - 2 qui donne 0, c'est à dire "rien du tout".
Donc il reste -1.
Autrement dit :
2 - 3 = 2 - 2 - 1 = -1 .
Ou, pour aller plus vite :
2 - 3 = -1 .
De la même manière, si nous avons à calculer 12 - 27 , nous pouvons nous dire que pour enlever 27, il faut d'abord enlever 12 puis ensuite enlever 15.
Nous pouvons donc écrire :
12 - 27 = 12 - 12 - 15
Et, comme 12 - 12 = 0, nous obtenons :
12 - 27 = -15
Ainsi nous avons maintenant le moyen d'effectuer "techniquement" des soustractions qui, autrefois, étaient jugées impossibles.
C'est maintenant l'heure d'un petit exercice...
A vous de jouer
En utilisant la méthode décrite ci-dessus, calculer les résultats des soustractions suivantes. (Passez votre souris sur les points d'interrogations pour vérifier vos réponses.)
a) 13 - 39 = ? b) 45 - 100 = ? c) 123 - 200 = ? d) 6 - 24 = ? e) 340 - 410 = ?
3ème partie - Un peu d'histoire...
Ces "simples" petits calculs, d'un niveau élémentaire, se comprennent généralement assez bien.
Cela explique pourquoi ce principe de calcul a été découvert très tôt dans l'histoire des hommes :
Déjà, au 1er siècle de notre ère, les chinois l'utilisait pour résoudre certains problèmes. Plus tard, on en trouva des traces en Inde. Et, enfin, cette pratique arriva en Europe...mais seulement vers le XVème siècle ! (On peu se demander pourquoi cette technique a mis si longtemps pour aller de l'Inde à l'Europe, mais c'est une autre "histoire"...)
Pour autant, ces nombres précédés d'un signe "-" n'ont pas été acceptés tout de suite car, s'il était possible de les expliquer "techniquement", leur "interprétation" restait difficile :
En effet, que pouvait signifier l'opération "2 morceaux de bois - 3 morceaux de bois" ?
La réponse à ce genre de question était loin d'avoir du sens, et il a fallu de longues, très longues années pour y parvenir.
Près de 300 ans en réalité.
Par ailleurs, ces nombres munis d'un signe "-", qu'on appellera "nombres négatifs", posaient des problèmes techniques dans certaines opérations (dans les multiplications, les divisions, les comparaisons), et ils semblaient se comporter très différemments des nombres "habituels".
Par exemple, comment comprendre la multiplication (- 2) × (- 3) ?
Quel interprétation lui donner ?
Et quel sera le résultat de cette opération ?
Il a fallu une réelle "révolution" dans la manière de voir les nombres, les mathématiques, et les sciences en général, pour passer ce cap.
Au cours de ces 300 années de discussions, recherches, inventions, beaucoup d'idées et de découvertes (ou de "re"-découvertes ?) eurent lieu.
Parmi elles, on peut noter celle des mathématiciens Wilkens (1800), Busset (1804) et Klostermann (1817) qui, peut-être gênés par ce signe "-" qui était, et est toujours, celui de la soustraction, écrivirent :
![]() .
.
Dans les années 1970, Kenneth R. Williams reprendra cette notation et la développera pour montrer combien elle peut être utile dans le calcul mental, toutes opérations confondues. C'est son travail qui est en partie utilisé dans les explications figurant sur notre site sous le nom de "nombres barrés".
Pour en apprendre davantage sur ces nombres, vous pouvez visiter la section "soustraction" du niveau 6ème.
4ème partie - Convention d'écriture
Puisque ce signe "-" devant un nombre a, historiquement, posé quelques problèmes, la convention suivante a été adoptée :
Quand un signe "-" n'est pas un signe de soustraction,on le met lui,
ainsi que le nombre qu'il accompagne,
à l'intérieur de deux parenthèses.
Ainsi, dans le calcul 2 - 3, on écrira 2 - 3 = (-1) au lieu de 2 - 3 = -1.
Nous appliquerons cette convention quelques temps, puis nous verrons un peu plus tard dans ce programme de 5ème comment nous en passer.
5ème partie - Interprétation "géométrique" de 2 - 3
1 - Rappels sur la soustraction
Certains professeurs des écoles enseignent à leur élèves que 3 - 2 peut se lire aussi "2 pour aller à 3".
Cette manière de lire "3 - 2" est intéressante car elle contient en elle une idée de "mouvement", c'est à dire un point de départ (le 2) et un point d'arrivée (le 3).
On peut alors imaginer une droite graduée et, si l'on note D le départ et A l'arrivée, nous obtenons quelque chose comme ceci :
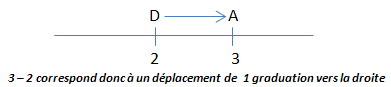
Autrement dit :
Toutes les soustractions "possibles" (où le 1er terme est plus grand que le 2ème),
peuvent être interprétées comme étant un déplacement vers la droite.
2 - Maintenant, regardons ce qui se passe quand nous avons une soustraction "impossible" comme "2 - 3"
Nous pouvons la lire "3 pour aller à 2", ce qui signifie que cette fois-ci, le point de départ D est sur le 3, tandis que le point d'arrivée A se trouve sur le 2.
Par un raisonnement analogue au précédent, nous obtenons le dessin suivant :
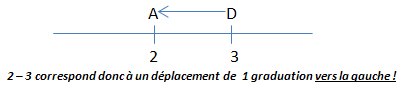
Par conséquent,
Nous pouvons interpréter toutes les soustractions "impossibles" (où le 1er terme est plus petit que le 2ème)
comme étant des déplacements vers la gauche !