Axes gradués et fractions

1ère partie - L'axe gradué

En mathématiques, un axe gradué est une droite "orientée "sur laquelle nous avons placé des graduations régulières correspondant aux nombres entiers et décimaux.

Par exemple, la droite suivante est un axe gradué : 

alors que celle-ci ne l'est pas (à cause de l'absence de la petite flèche à droite) :

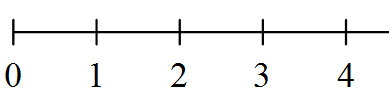
La droite suivante n'est pas un axe gradué (à cause des graduations irrégulières) :

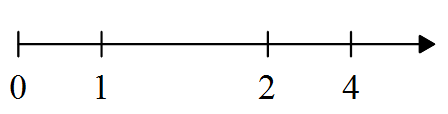
Par contre, la suivante l'est (car elle contient des graduations régulières et une petite flèche (à gauche)) :

La petite flèche (à gauche ou à droite) n'est pas là pour décorer le dessin. Sa signification est importante. Elle signifie que plus on va dans le sens de la flèche, plus les nombres sont grands (et donc, plus on va à l'opposé de la flèche, plus les nombres sont petits) :

2ème partie - Placement d'un point sur un axe gradué

Dans cette partie, la géométrie commence à cotoyer le calcul...

En géométrie, l'emplacement d'un point est symbolisé par une croix. Par exemple, si nous voulons placer un point A au centre de cette page, nous dessinons une croix et nous plaçons la lettre A majuscule juste à côté de cette croix : 

Nous suivrons donc le même principe si nous voulons placer un point a sur un axe gradué : à l'endroit désiré, nous tracerons une croix sur l'axe gradué, et mettrons la lettre A majuscule au dessus de la croix :

Dans cet exemple, nous avons placé le point A juste sur la graduation 5 . Nous disons alors que l'abscisse de Aest 5 et nous écrirons A(5).

Si nous voulons placer B(3,5) nous ferons de même mais il faudra imaginer, ou tracer, les "demi " graduations afin d'obtenir un dessin précis : on compte à partir du 0 jusqu'à 3,5 et là, on place le point B .

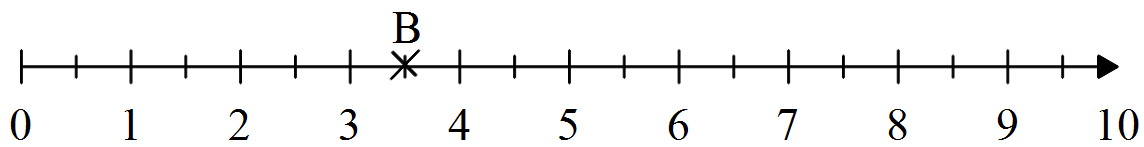
De même, si nous voulons placer le point C(0,3) nous serons obligés de tracer les graduations correspondant aux "dixièmes" puis de chercher le 3ème dixième afin d'obtenir un dessin précis :

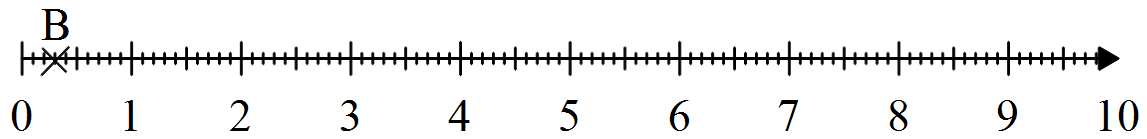
3ème partie - Et quand les abscisses sont des fractions, comment faire ?

 

Et si nous devions placer le point D(), comment devrions-nous faire ?

Ici, il faut se souvenir de la signification de cette fraction : .

Elle signifie, par exemples :

- le partage de 1 en trois parts égales,

- ou bien encore le fait de diviser quelque chose par 3 et de prendre une des parts découpées.

- ou bien de penser au quotient de 1÷ 3 (comme si la division se terminait par un reste nul). Ce quotient est d'environ 0,333...qu'il suffit alors de répérer sur l'axe gradué (quelque part entre 0 et 1...).

Si nous ramenions ces trois interprétations à la situation qui nous occupe actuellement, nous pourrions dire :

C'est le partage de la graduation 1 en trois parts égales, chacune d'elles faisant environ 0,333...

De la même manière, si nous devions placer le point D(), nous pourrions penser à :

- diviser le segment formé par les 10 premières graduations en 3 parts égales,

- ou bien calculer le quotient 10 ÷ 3 (en faisant comme si la division se terminait par un reste nul), trouver environ 3,33... puis chercher où il se trouve sur l'axe gradué,

- ou bien diviser toutes les graduations en 3 parts égales  puis, à partir du 0 de l'axe gradué , reporter 10 de ces parts et, enfin, placer E au point d'arrivée,

- etc.

Il y a beaucoup d'interprétations possibles pour ce genre d'activité. Il suffit d'en choisir une correspondant à un partage de "quelque chose" qui fait 10 en trois parts égales :

4ème partie - A quoi servent les axes gradués quand on a des fractions ?

Utilité n°1 - La comparaison de fractions

Nous avons vu, dans la section sur la comparaison des fractions, un certain nombre de stratégies pour y arriver. Et bien les axes gradués nous permettent d'ajouter une nouvelle méthode pour comparer des fractions :

Pour comparer deux fractions, il suffit de penser que ces deux fractions sont des abscisses de points.

On place les deux points sur un axe gradué,

et le point le plus à gauche (ou le plus proche de 0) correspond à la fraction la plus petite.

Utilité n°2 - La compréhension des évènements de la vie quotidienne

Il n'est pas rare, dans la vie quotidienne, d'entendre les gens parler en utilisant des fractions :

- "Il est sept heures et quart",

- "J'arrive dans une-demi heure",

- "J'ai mangé un quatre quarts",

- "C'est la mi-temps",

Les exemples sont trop nombreux pour les citer tous.

Les exemples cités ici ont tous plusieurs points communs : ils utilisent des sous-entendus qu'il faut savoir/apprendre à "percevoir".

1) Par exemple, dans "Il est sept heures et quart" , il faut comprendre "Il est sept heures et un quart d'heure" qui sous-entend qu'on doit ajouter "un quart d'une heure" aux sept heures. Nous devrons donc calculer (ou connaître) le résultat de "un quart d'une heure", soit "un quart de 60 minutes". Il nous faut donc diviser 60 minutes en 4 parts égales, ce qui donne 15 minutes. Donc "Il est sept heures et quart" signifie "Il est sept heures et 15 minutes".

2) De même, dans "C'est lami-temps", il faut comprendre "c'est la moitié du temps réglementaire qui s'est écoulée". Il faudra donc connaître (calculer) la moitié de ce temps réglementaire. S'il fait 90 min, on calculera 90 minutes ÷ 2 = 45 minutes.

Pour plus de détails sur ce genres de calculs, vous pouvez vous rendre à la section "Fraction d'une quantité".