Division avec diviseur à un chiffre
Puisque la division par 9 a été vue dans les deux sections précédentes, nous allons voir maintenant comment diviser un nombre par un diviseur à un chiffre différent de 9 (qui sera donc 2, 3, 4, 5, 6, 7 ou 8).
1ère partie - Avec un dividende à deux chiffres
Méthode traditionnelle
Prenons par 43 divisé par 7 (noté aussi 43 : 7).
Selon la tradition, il est de coutume de poser ce genre de division comme ceci :

Rappelons que diviser 43 par 7 revient à se demander combien de fois nous devrons ajouter de 7 ensemble afin d'arriver le plus près possible de 43.
Cette façon d'ajouter plusieurs 7 ensemble nous fait immédiatement penser à la multiplication .
Par conséquent, nous devons utiliser la table de multiplication de 7.
Dans celle-ci, le nombre inférieur à 43 mais le plus proche possible de 43 est 42 obtenu en faisant 6 x 7. Et comme 43 - 42 = 1, nous écrivons :
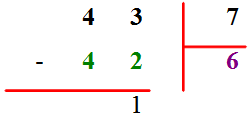
Les personnes capables de gérer à la fois la recherche du 42 = 6 x 7 et la soustraction 43 - 42 = 1 écrirons la version simplifiée suivante :
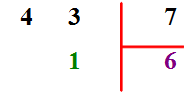
Le bilan est donc que 6 x 7 + 1 = 43.
6 est appelé le quotient et 1 le reste, tandis que 43 était le dividende et 7 le diviseur.
(Petite astuce mnémotechnique: pour éviter de mélanger diviseur et quotient : diviseur et dividende commencent tous les deux par la lettre d et son placés au dessus du quotient et du reste).
Méthode proposée
Il ne s'agit pas, à proprement parler, d'une autre méthode mais plutôt d'une autre manière de présenter la division. Dans le cas de 43 divisé par 7, nous proposons de poser la division de la manière suivante :

(en faisant attention de placer le 6 sous le 3 de 43 !)
La conslusion est donc que 6 x 7 + 1 = 43.
Le raisonnement est le même que celui décrit dans la méthode traditionnelle.
Nous verrons plus loin l'avantage de cette présentation par rapport à celle de la méthode traditionnelle.
2ème partie 2 - Avec un dividende à plus de deux chiffres
Méthode traditionnelle
Prenons par 259 divisé par 6 (noté aussi 259 : 6).
Selon la tradition, nous poserons la division comme ceci :
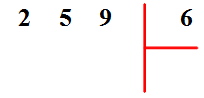
1ère stratégie
En suivant le même type de raisonnement que dans la Partie 1, nous savons que nous devons utiliser la table de multiplication de 6.
"Combien de 6 devons-nous ajouter ensemble de manière à arriver le plus près possible de 259 (et si on pouvait même obtenir exactement 259, ce serait encore mieux car comme ça, nous aurions un reste égal à 0)" ?
Comme, généralement, et dans le meilleur des cas, nous avons appris la table de 6 jusqu'à 10 x 6 = 60, nous voyons qu'il nous faudra beaucoup plus que 10 "six" pour arriver à 259.
A l'évidence, nous n'allons pas nous amuser à chercher la réponse en nous demandant ce que donne 11 x 6, 12 x 6, etc. Ce serait très long et bien peu passionnant.
2ème stratégie
Nous pourrions découper 259 et penser qu'il peut s'écrire 200 + 59. Ainsi, diviser 259 par 6 reviendrait à diviser 200 par 6 puis 59 par 6. Nous pouvons facilement voir que 59 : 6 donnera environ 9, mais par contre 200 : 6 reste hors de portée de notre misérable petite table de 6.
3ème stratégie (la meilleure car la plus efficace)
Si le découpage précédent s'est révélé insuffisant, peut-être est-ce parce qu'il était mal pensé.
Nous pourrions aussi nous dire que 259 est équivalent à 25x 10 + 9 , ou encore à 25 dizaines et 9 unités.
Donc 259 : 6 reviendrai à diviser 25 dizaines en 6 parts, puis à diviser 9unités en 6 parts.
Or,diviser 25 dizaines en 6 parts revient à chercher à diviser 25 en 6 parts, comme çà, nous saurons combien de dizainesil y aura dans chaque part !
Cela signifie donc que le quotient contiendra des dizaines et des unités. Il aura donc deux chiffres !
C'est la raison pour laquelle nous écrivons traditionnellement ceci (ou quelque chose d'approchant) :
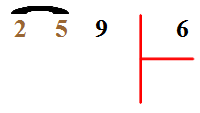
La table de 6 nous permet de voir que le résultat le plus proche de 25, en étant plus petit ou égal à 25, est 24, obtenu par 4 x 6. Et comme 25 - 24 = 1, nous écrivons :
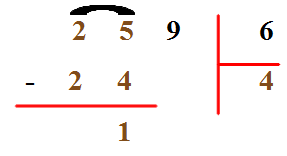
Arrivés à ce stade, nous devons avoir à l'esprit que ce 1 indique qu'il reste 1dizaine que nous devons ajouter aux 9 unités restantes. Autrement dit, nous devons maintenant diviser 1 9 par 6. L'apparition de ce 19 est matérialisée en imaginant que le 9 du 259 descend pour se placer à la droite du 1 :
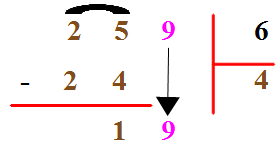
La table de 6 nous permet de voir que le résultat le plus proche de 19 , en étant plus petit ou égal à 19 , est 18, obtenu par 3 x 6. Et comme 19 - 18 = 1, nous écrivons :

C'est la solution la plus complète enseignée traditionnellement aux élèves des écoles et collèges. L'écriture des soustractions est facultative et la version abrégée suivante est souvent préféré par les personnes sachant gérer les tables et les soustractions de tête :
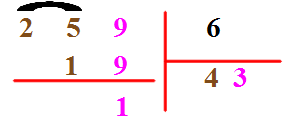
La conclusion est donc que 43 x 6 + 1 = 259.
Bilan provisoire
Très technique, la division nécessite de bien connaitre les tables de multiplications, de gérer des soustractions avec des termes à deux chiffres, parfois trois, et oblige sans cesse la personne qui la pose à alterner d'un côté et de l'autre, en écrivant tours à tours les différents chiffres du quotient et du reste, tout en pensant à faire "descendre" certains chiffres afin de pouvoir continuer la division jusqu'au bout. Cet ensemble de contraintes ne laisse aucun répit. Elle met rapidement n'importe quel individu en surcharge intellectuelle, et c'est sans doute la raison pour laquelle la division est tant redoutée par les collégiens.
Méthode/présentation proposée
(La suite de cet article n'est accessible qu'aux abonnés.)
Quand on connait la meilleure stratégie, pourquoi continuer à la compliquer avec une mise en page si complexe, et si gourmande en espace ?
Posons-nous la bonne question : Quelles sont les priorités dans une division ?
La réponse est : Connaitre ses tables et faire des soustractions !
Autrement dit, passer de gauche à droite, et penser à faire "descendre" des chiffres sont des actions que nous devons éviter !
Comment ?
En posant la division comme ceci :
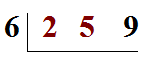
La stratégie étant la même, nous savons que dans 25, il peut y avoir au maximum 4 "six" et qu'il restera 1. Nous allons donc écrire :
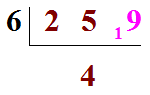
(en plaçant bien le chiffre 4 sous le 5 du 25 - c'est le seul "souci" que nous devons avoir :-) )
Et comme dans 19 il ne peut y avoir au maximum que 3 "six" et qu'il restera 1, nous allons écrire :
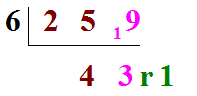
Bilan
Avec cette manière de poser la division, tout se passe du côté droit, et nous n'avons eu aucun chiffre à "descendre". La charge de travail intellectuel a donc diminué de moitié et, mieux encore, cette présentation condensée permet à court terme de savoir gérer mentalement des divisions complexes.
Un dernier exemple, en image
Prenons la division de 86 724 par 8.
La 1ère étape de notre stratégie est de considérer uniquement le 8 du 86 724. Nous obtenons :
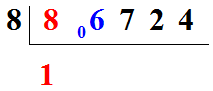
Puis, sachant que 06, c'est à dire 6, ne contient aucun 8, et qu'il reste donc 6, nous aurons :
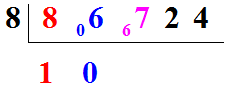
Puis, sachant que dans 67 il y a 8"huit" et qu'il reste 3, nous aurons :
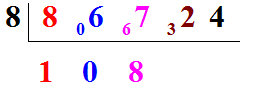
Et dans 32 , il y a 4"huit" et il reste 0 :
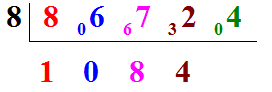
Et enfin, dans 04 , il n'y a aucun8 et il reste 4 :
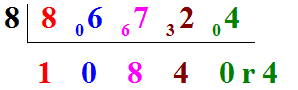
Conclusion : 86 724 = 10 840 x 8 + 4.
"Innover, ce n'est pas avoir une nouvelle idée mais arrêter d'avoir une vieille idée."