Cette section fait suite à celle sur la division. Il est donc fortement recommandé de maîtriser la technique de la division, qu'elle soit euclidienne ou décimale.

1ère partie - Fractions unitaires

Dans l'Egypte (très) ancienne, les fractions unitaires étaient déjà connues et utilisées.

Les fractions unitaires sont des fractions dans lesquelles le numérateur est toujours égale à ... 1 alors que le dénominateur peut être n'importe quel nombre entier .

Par exemple, 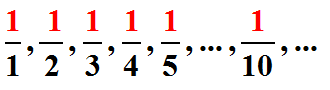$repfraction-001$ sont des fractions unitaires. En plus d'avoir un intérêt historique, ces fractions portent des noms particuliers qui servent à nommer toutes les autres fractions :

- Ainsi, $repfraction-002$ , qui correspond à la division de 1par 1, et qui donne comme quotient 1, est appelée la fraction unité.

. . .

- La fraction $repfraction-003$ , qui correspond à la division de 1 par 2, et qui donne comme quotient 0,5 est lue "un-demi". Ainsi, toutes les fractions ayant 2 au dénominateur auront un nom qui finira par "demi".

. . .

- La fraction $repfraction-004$ , qui correspond à la division de 1 par 3, et qui donne comme quotient approché 0,333... est lue "un-tiers". Ainsi, toutes les fractions ayant 3 au dénominateur auront un nom qui finira par "tiers".

. . .

-La fraction $repfraction-005$ , qui correspond à la division de 1 par 4, et qui donne comme quotient 0,25 est lue "un-quart" . Ainsi, toutes les fractions ayant 4 au dénominateur auront un nom qui finira par "quart".

. . .

- La fraction $repfraction-006$ , qui correspond à la division de1 par 5, et qui donne comme quotient 0,2 est lue "un-cinquième" . Ainsi, toutes les fractions ayant 5 au dénominateur auront un nom qui finira par "cinquième".

. . .

- Pour toutes les fractions suivantes, on appliquera la même règle de lecture que pour $repfraction-006$ .

Mais que signifie le 1 du numérateur ?

Quand le 1 apparait au numérateur des fractions, il peut signifier plusieurs choses :

a) Si nous nous rappelons la signification des mots "numérateur" et "dénominateur", ce 1 va indiquer qu'on prend une part parmi toutes celles qui ont été faites dans le partage "parfait" représenté par la fraction.

Ainsi, dans $repfraction-006$

le 5 désigne le nombre de parts faites lors du partage,

et le 1 indique qu'on prend une part parmi les 5 possibles.

b) Mais ce 1 peut signifier aussi "une part d'un objet" qu'on aura divisé en plusieurs parts égales, et ce quel que soit cet "objet".

Ainsi, dans $repfraction-006$

le 5 désigne le nombre de parts faites lors du partage,

et le 1 indique qu'on prend une part (d'un objet)

parmi les 5 possibles.

Par exemple, si nous avons une bande de papier de n'importe quelle longueur, et que nous voulons en découper $repfraction-006$ , cela signifiera que nous devrons mesurer notre bande de papier, diviser cette mesure en 5 parts égales et en prendre une part.

2ème partie - Les différentes représentations graphiques d'une fraction unitaire

Le "camembert" ? ou bien le rectangle ? ou alors le carré ? ou alors ...

Suppososns que nous voulions illustrer la fraction $repfraction-004$ .

1°) Nous pourrions imaginer que nous avons un disque, que nous le partagions en 3 parts égales, et que nous en examinions 1 part. Cela nous donnerait quelque chose comme ceci, 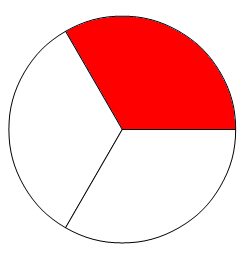$repfraction-007$ où la part rouge désigne le 1 du numérateur.

2°) Nous pourrions aussi imaginer un rectangle découpé en 3 parts égales, et dans lequel nous prendrions 1 part : $repfraction-008$

3°) Nous pourrions aussi imaginer un demi-disque, découpé lui aussi en trois parts égales dans lequel nous prendrions 1 part : 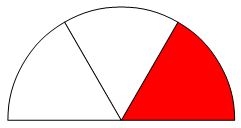$repfraction-009$

4°) Nous pourrions aussi choisir de prendre un segment, un simple segment, de disons 6 cm, que nous découperions en 3 parts égales, et où nous mettrions en évidence, avec une couleur particulière, la part que nous comptons prélever : $repfraction-010$

5°) En fait, nous pourrions imaginer "n'importe quoi", pour peu qu'il soit facilement découpable en autant de parts égales que nous le souhaitons, et nous mettrions en évidence, avec une couleur particulière, la part de ce "n'importe quoi" que nous comptons prélever.

3ème partie - Les fractions autres que les fractions unitaires

Une fraction est créée en utilisant deux nombres entiers, l'un au numérateur, l'autre au dénominateur.

Nous avons donc deux possibilités :

Soit le numérateur est plus petit que le dénominateur ;
Soit le numérateur qui est plus grand que le dénominateur.

Examinons le 1er cas : Prenons la fraction $repfraction-011$ .

Selon la Partie 2, nous savons que nous pouvons imaginer n'importe quoi (disons un disque), en le découpant en 7 parts égales, puis en "coloriant" 4 de ces parts. Nous allons obtenir ceci :

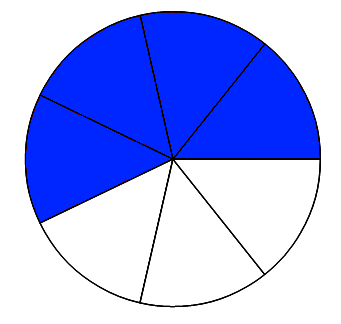
$repfraction-012$

La méthode d'illustration donnée en Partie 2 fonctionne donc très bien dans le cas où le numérateur est plus petit que le dénominateur.

Nous voyons qu'une telle fraction est toujours représentée par un dessin qui n'est pas totalement colorié !

De plus, si nous faisons la division du numérateur par le dénominateur, nous verrons que le quotient commence toujours par 0,.... Le quotient est donc plus petit que 1, c'est à dire que nous avons besoin de coloriér une partie de l'objet.

Examinons maintenant le 2ème cas : Prenons la fraction $repfraction-013$ .

Cette fois-ci, le problème est différent car si l'objet que nous choisissons est découpé en 7 parts égales, il nous sera impossible d'en prendre 9 ! Alors comment l'illustrer par un dessin ?

En fait, il suffit de "décomposer" le 9 : Pour prendre 9 parts, il faudrait en prendre d'abord 7, puis 2.

Il nous sera facile de prendre 7 parts si nous avons partagé en 7 parts égales. Les 2 dernières semblent cependant poser un problème car elles n'existent pas !

Mais au fait, pour prendre à nouveau 2 parts, il nous faut un autre objet, identique au premier, découpé lui aussi en 7 parts égales,dans lequel nous irons prendre les deux parts qui nous manquent !

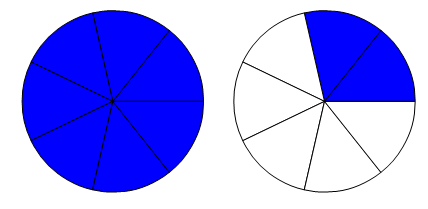Nous aurons donc : $repfraction-013$ qui sera équivalent à $repfraction-014$ auquel nous ajouterons $repfraction-015$ , ce qui nous donnera l'illustration $repfraction-016$ .

Dans ce cas-là, il faut penser à utiliser plusieurs fois le même objetà cause de la décomposition que nous sommes obligés de faire au numérateur.

De plus,si nous effectuons la division du numérateur par le dénominateur, nous verrons que le quotient est toujours plus grand que 1, ce qui veut dire plus grand qu'un objet (donc 2 objets, ou 3, ou 4, etc. devront être utilisés).

| Mention légale |