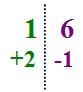Les Nombres Barrés (1/2)

Ce chapitre nécessite la maîtrise absolue des compléments à 9 et à 10, ainsi que de la méthode de soustraction utilisant ces compléments.

1ère partie - Les nombres barrés, qu'est-ce que c'est ?

Un nombre barré correspond en réalité à une autre manière d'écrire un certain type de soustractions.

Exemple 1 : Le nombre 19, proche de 20, est égal à 20 – 1. En « contractant » cette soustraction, on va écrire :

Ainsi, comme on le voit, l'opération 20 - 1 est "contractée" en remplaçant le "0" du 20 par le 1 situé après le signe de la soustraction et, pour ne pas confondre avec le nombre 21, on a placé une barre au dessus du 1 (on pourrait imaginer que le signe "-" de la soustraction est venu se placer au dessus du 1).

La contraction obtenue se lira "Deux barre un".

Remarque :  Seul un zéro situé dans le 1er terme de la soustraction sera remplacé par un chiffre barré.

2ème partie - Un nombre possède-t-il plusieurs formes barrées ?

Exemple 2 : Prenons le nombre 19. Il peut être obtenu, entre autres, par les soustractions suivantes : 

19 = 20 - 1

19 = 100 - 81

19 = 1000 - 981

etc. 

En suivant le même raisonnement que dans la 1ère partie, nous pourrons écrire : 

  Cet exemple nous permet de voir que : 

• nous pouvons avoir plusieurs chiffres sous une barre ;
• le même nombre (ici, le 19) peut avoir plusieurs équivalents barrés .
  

• 
  

3ème partie - La barre doit-elle être toujours placée au dessus des derniers chiffres ?

 (La suite de cet article n'est visible que par les utilisateurs enregistrés.)