Définition : Une fraction décimale est une fraction dont le dénominateur est une "puissance de 10" (c'est à dire que le dénominateur peut être 1, 10, 100, 1000, etc.).

Donc $compfractions-008$ , $compfractions-009$ , $compfractions-010$ , $compfractions-011$ , ou même $compfractions-012$ sont des fractions décimales.

En fait, peu importe ce qu'il y a au numérateur, l'essentiel est qu'au dénominateur il y ait une "puissance de 10".

Ainsi, même 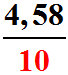$compfractions-013$ peut être considérée comme une fraction décimale !

Pour quelle raison ces fractions sont-elles appelées "décimales" ?

Et bien, c'est parce qu'elles ont un lien avec les nombres décimaux. C'est ce que nous allons voir maintenant...

2ème partie - Liens avec les nombres décimaux

Dans la section sur la division, nous avons rappelé le principe de la division par 10, par 100, par 1000, etc.
De plus, nous savons qu'une fraction n'est rien d'autre qu'une division où le reste vaut 0.

Ces deux idées mises en commun nous permettent de voir qu'une fraction décimale est appelée décimale parce que son quotient est un nombre décimal !

Ainsi, $compfractions-009$ correspond à la division de 4 par 10, et en vertu de ce que nous savons sur la division par 10, le quotient sera 0,4 qui est bien un nombre décimal !

De même 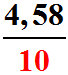$compfractions-013$ correspond à la division de 4,58 par 10 et donnera un quotient de 0,458 !

Le cas de $compfractions-008$ ne fait pas exception à la règle. La division de 3 par 1 donne un quotient de 3, qui pourrait très bien s'écrire 3,0 et qui est bien un décimal lui aussi.

3ème partie - Décompositions d'un nombre décimal

Le lien entre les fractions décimales et les nombres décimaux est l'occasion de s'entrainer à passer de l'un à l'autre.

1) D'un nombre décimal à ses décompositions en fractions décimales.

Exemple : Considérons le nombre décimal 15, 379 .

a) Conversion en une fraction décimale unique

Dans 15,379 nous voyons que le dernier chiffre de la partie décimale, le 9, est dans la position des millièmes.

Donc nous pouvons convertir ce nombre décimal en fraction décimale où le dénominateur sera 1000.

Pour y arriver, il nous suffit de supprimer la virgule à 15,379 , qui va donc devenir 15379, puis de le placer au numérateur de notre fraction, pendant que nous placerons le 1 000au dénominateur.

Donc 15, 379 = 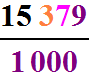$compfractions-014$ .

b) Conversion en "partie entière" + fraction décimale unique.

Nous pourrions aussi voir 15,379 comme 15 + 0,379 .

Or 0,379 n'est rien d'autre que le nombre 379 où la virgule (placée à droite du 9mais pas écrite) aurait été décalée de trois chiffres vers la gauche.

Autrement 0,379 n'est rien d'autre que379 ÷ 1 000.

Donc 15 + 0,379 = 15 + 379 ÷ 1 000 = 15 + 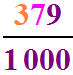$compfractions-015$ .

c) Conversion en "partie entière" + une fraction décimale par chiffre de la partie décimale.

Nous pourrions aussi voir 15,379 comme 15 unités et 3 dixièmes et 7 centièmes et 9 millièmes.

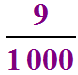Or 3 dixièmes s'écrit $compfractions-016$ , 7 centièmes s'écrit $compfractions-017$ , et 9 millièmes s'éc rit $compfractions-018$ .

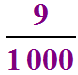Donc 15,379 = 15 unités et 3 dixièmes et 7 centièmes et 9 millièmes = 15 + $compfractions-016$ + $compfractions-017$ + $compfractions-018$ .

d) Autres décompositions possibles

Il existe encore beaucoup d'autres manières différentes de voir le nombre 15,379 .

Par exemple, nous pourrions le voir comme 15 + 0,3 7 + 0,00 9 .

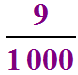Or 0,3 7 s'écrit $compfractions-019$ et 0,00 9 s'écrit encore $compfractions-018$ .

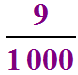Donc 15,379 = 15 + 0,3 7 + 0,00 9 = 15 + $compfractions-019$ + $compfractions-018$ .

Mais nous pourrions aussi écrire 15,379 sous la forme 15 + 0,3 + 0,079, etc.

2) Des fractions décimales aux nombres décimaux.

Il s'agit de l'inverse de ce qui précède, à ceci près que parfois, les fractions ne sont pas écrites dans le bon ordre...

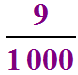Par exemple, si nous avons le l'expression $compfractions-009$ + 5 + $compfractions-018$ ,

il faut bien penser à tout remettre dans le "bon" ordre,

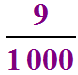
y voir en fait 5 + $compfractions-009$ + $compfractions-018$

qui se converti ensuite facilement en 5,409 !

4ème partie - Les fractions sur 100

Les fractions ayant 100 au dénominateur sont particulièrement fréquentes de nos jours (TV, Internet, radios fm, journaux écrits).

Elles portent d'ailleurs un nom bien particulier : les pourcentages .

Par exemple, $compfractions-019$ se lira très fréquemment "37 pour cent" et s'écrira généralement "37%" au lieu de "37 sur 100" ou "37 centièmes", même si les deux dernières manières de parler sont tout à fait correctes et acceptables.

De même $compfractions-017$ se lira volontier "7 pour cent" et s'écrira "7%".

En fait, le symbole "%" remplace " $compfractions-020$ ".

Remarque :

Dans les journaux écrits, ou dans les statistiques réalisés dans n'importe quels domaines, les pourcentages ne s'écrivent quasiment jamais sous forme de fractions.

Au lieu de cela, on leur préfère une autre notation, utilisant le symbole "%" qui signifie "pour cent".

Ainsi, on ne verra jamais écrit dans un quotidien la phrase :

" $compfractions-019$ des consommateurs regardent la TV plus de 4h par jour".

A la place, on verra écrit :

"37% des consommateurs regardent la TV plus de 4h par jour".

La raison de l'existence et l'utilisation du symbole "%" est facile à comprendre : l'écriture en fraction prend de la place et oblige à choisir un interligne plus grand, or dans un quotidien, pour limiter le coût d'impression, chaque espace économisé signifie au final une page (ou plusieurs) d'économisées.

Les pourcentages sont souvent employés dans les médias afin de "gonfler" un peu certains nombres, et transformer ainsi (parfois beaucoup) la réalité des faits :

Petite anecdote sur les pourcentages

Dans une petite ville, Yannick faisait parti d'un petit club de tir à la carabine. Au total, le club comptait 30 adhérents. Parmis ces adhérents, 4 furent qualifiés au Championnat de France de leur discipline. Yannick fut chargé d'écrire un article sur ce sujet afin de le transmettre au quotidien local. Afin de faire pâraître le club de tir local comme "plus important" que ce qu'il était en réalité, il écrivit : "Le club de tir [...] a vu 14% de ses tireurs qualifiés pour le Championnat de France !"

Nous verrons, dans la section "Fractions égales - Proportionnalité", comment utiliser les pourcentages (niveau 6ème).

Au niveau 5ème, les calculs de pourcentages sont au programme en mathématiques.

5ème partie - Les fractions sur 15 000, 25 000, etc.

Des dénominateurs très "grands" sont visibles dans certains domaines :

les cartes IGN (on peut rencontrer des dénominateurs voisins de 15 000, voir de 25 000 pour des cartes très précises sur des zones géographiques très ciblées).ou encore dans tout ce qui est réduction de dimension (maquettes, plans, etc).

Dans tout ce qui est réduction de dimensions (maquettes, plans, modèles réduits, etc). Dans ces cas là, les dénominateurs peuvent être de 40, 50 ou bien plus.

On ne parle plus alors de fractions, mais d'échelles.

L'utilisation d'échelles n'est pas au programme de 6ème, mais à celui de 5ème.

La notion d'échelle est liée à celle de la proportionnalité : elle se retrouve à tous les niveaux du collège, sous différentes formes (calculs, géométrie).

| Mention légale |