La division décimale par 9
Cette section demande une bonne connaissance de la structure des nombres entiers et décimaux, de la division par 10, et de la division par euclidienne par 9.
1ère partie - Une division décimale par 9 (exemple basique)
Supposons que l'on désire calculer 123 ÷ 9 et nous voulons un quotient décimal qui possède un chiffre après la virgule.
Nous allons, comme dans la division euclidienne par 9, la poser comme ceci :
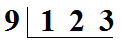
Puisque 9 est proche de 10, et parce que nous savons que la division par 10 entraine un décalage de la virgule de un chiffre vers la gauche, nous pouvons considérer qu'il va se passer la même chose dans la division par 9. Autrement dit, le quotient aura une partie entière qui possèdera un chiffre de moins que la partie entière de 123 : nous allons donc placer tout de suite la virgule au bon endroit, c'est à dire entre le 2 et le 3.

Maintenant nous allons effectuer la division décimale exactement comme nous effectuions la division euclidienne par 9.
1ère étape : Le 1 de 123 est aussi le 1er chiffre du quotient :

2ème étape : Nous ajoutons le 1 avec le 2 de 123. Nous trouvons 3. C'est le 2ème chiffre du quotient :
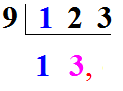
3ème étape : Nous ajoutons le 3 de l'étape précédente avec le 3 du 123. Nous obtenons 6. C'est le 1er chiffre de la partie décimale du quotient :

Donc 123 ÷ 9 ≈ 13,6 au dixième près.
.2ème partie - Division décimale par 9 (cas "complexe")
(La suite de cet article n'est accessible qu'aux abonnés)