Division euclidienne avec diviseur à un chiffre.
Par définition, la division intervient quand on désire effectuer un partage en parts égales.
Une division devient euclidienne si :
son dividende, son diviseur, son quotient et son reste
sont tous les quatres des nombres entiers ,
De plus, il existe une petite contrainte supplémentaire sur le reste :
Le reste doit être strictement inférieur au diviseur .
Ainsi, si on considère le partage de 30 en 7 parts égales, nous pourrions avoir :
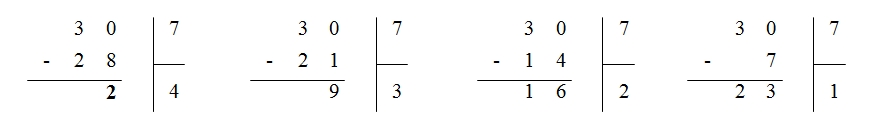
Mais parmi toutes ces divisions, qui mathématiquement sont vraies, seule la première représente une division euclidienne car c’est celle qui correspond à un « partage complet » de 30 en 7 paquets contenant chacun 4 éléments, et un reste de deux éléments qui ne peut être réparti au risque de rendre ce partage inégal.
Si l’idée qui se cache derrière la division euclidienne est assez simple (un partage total en parts égales), la technique généralement enseignée et apprise pour efectuer ce partage pose parfois quelques problèmes : demandez donc à un élève de 3ème de poser une division, vous allez vite le voir se décomposer devant vous.
Les raisons de cet échec fréquent ?
- D’une part le manque d’entrainement (parce qu’il est rare qu’une division soit à effectuer en 5ème ou en 4ème car d’une part les fractions font leur apparition, mais surtout parce que les calculatrices sont rapidement sorties lors du moindre calcul à faire !).
- D’autre part parce que la technique de la division elle-même pose des problèmes : poser la division de 6 412 par 76 revient à chercher plus ou moins dans la table de 76…ce qui devient très vite rébarbatif.
Et s’il existait d’autres méthodes pour y parvenir ?
Et si finalement la division n’était pas si terrible ?
Dans le menu de gauche, vous pouvez commencer par toucher du doigt le principe de la division exposé sur notre site : la division par 9, puis la division par 11 sont d’excellents moyens de se faire la main tranquillement.
Ensuite, nous passerons aux choses sérieuses…mais pas plus compliquées.
Bonne découverte ...
L'équipe de VAK-Conseil.