Cette section fait suite à celle sur la division. Il est donc fortement recommandé de maîtriser la technique de la division, qu'elle soit euclidienne ou décimale.

1ère partie - De la division euclidienne à la fraction.

Pour qui connait bien ses tables de multiplications, 3x5 donne immédiatement 15 . Nous avons vu, dans la section sur la division, que 3x5 = 15 permet de dire que 15÷5 = 3 (reste = 0) ou que 15÷3 = 5 (reste = 0), ce qui, à la manière traditionnelle, peut s'écrire :

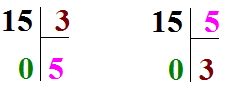
$divtofraction-001$

Dans la première division, 5 est le quotient de 15÷3 alors que dans la deuxième c'est 3 qui est le quotient de 15÷5.

Le fait que le reste soit 0, s'il est important de le savoir, n'a, en lui-même que peut d'intérêt. La division "tombe juste" et ce sont les valeurs des quotients possibles qui, généralement, nous intéressent dans le cas d'un partage.

Par conséquent, écrire ces divisions avec le 0 devient "inutile" puisque toute l'information utile est contenue dans les nombres 15, 3 et 5.

Ainsi, puisque "5 est le quotient de 15÷3 ", nous écrirons 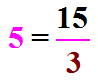$divtofraction-002$ .

Ou encore, puisque "3 qui est le quotient de 15÷5 " nous écrirons 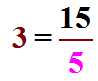$divtofraction-003$ .

Le symbole " = " n'est pas écrit pour "faire joli".

Il signifie que si "5 est un quotient de 15÷3 ", alors 15÷3 est aussi un quotient !

De la même manière, si "3 qui est le quotient de 15÷5 " alors cela signifie que 15÷5 est aussi un quotient !

Important : $divtofraction-004$ et $divtofraction-005$ sont appélées des fractions.

En résumé

3x5 = 15

est équivalent à

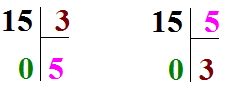
$divtofraction-001$

est équivalent à

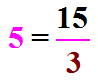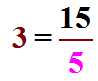
$divtofraction-002$ et à $divtofraction-003$

Une fraction n'est rien d'autre qu'une division dans laquelle le reste (qu'on n'écrit jamais) vaut 0.

. Vocabulaire à connaître

a) Quelques rappels tout d'abord :

Dans 3x5 = 15 , on dit que 3 et 5 sont des facteurs, et que 3x5 et 15 sont leur produit.

3x5 = 15 , on dit que 3 et 5 sont des diviseurs de 15.

b) Sur les fractions maintenant :

$divtofraction-004$ et $divtofraction-005$ sont appélées des fractions.

Dans 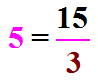$divtofraction-002$ , on dit que 5 et $divtofraction-004$ sont tous les deuxle quotient de 15 par 3.

Dans 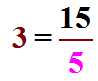$divtofraction-003$ on dit que 3 et $divtofraction-005$ sont tous les deuxle quotient de 15 par 5.

Dans la fraction $divtofraction-004$ on dit que 15 est le numérateur, alors que 3 est son dénominateur.

Dans la fraction $divtofraction-005$ on dit que 15 est le numérateur et que 5 est son dénominateur.

. Etymologie

Numérateur vient du latin "numerator" qui signifie "celui qui compte". Cela sera utile à connaître quand nous en viendrons à la section sur les diverses représentations d'une fraction.

Dénominateur vient du latin "denominator" qui signifie "celui qui désigne". Dans le cas des fractions, il désignera le nombre de parts faites. Là encore, ce sera utile à connaître quand nous en viendrons à la section sur les diverses représentations d'une fraction.

Remarque : Dénominateur et Diviseur commencent tous les deux par la lettre "D" et sont placés en "Dessous" dans une fraction.

2ème partie - De la division décimale à la fraction

1er cas : Lorsque le reste est nul

Dans la section sur la division décimale, nous avons vu qu'il est parfois possible d'obtenir un reste nul. Par exemple, dans 17 ÷ 2 = 8,5 nous avons bien un reste nul puisque 8,5 x 2 = 17.

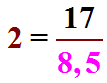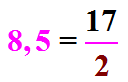Selon la Partie 1 , nous pouvons donc dire que 8,5 x 2 = 17 est équivalent à dire que $divtofraction-006$ ou que $divtofraction-007$ .

De même, dans 6,21 ÷ 2,3 = 2,7 nous avons bien un reste nul car 2,3 x 2,7 = 6,21 (pour plus de détails sur la manière de faire ce calcul rapidement, voir ici).

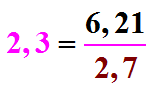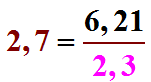Nous aurons donc là encore $divtofraction-008$ ou bien $divtofraction-009$ .

Par conséquent, quand le reste d'une division est nul, qu'il y ait des nombres décimaux ou non ne change rien car on peut toujours en tirer deux fractions.

2ème cas : Lorsque le reste n'est pas nul.

Le problème est que parfois la division "ne tombe pas juste" c'est à dire qu'il nous est impossible d'obtenir un 0 au reste. C'est le cas des divisions qui "ne finissent jamais" comme 10÷3 par exemple. Si nous posions la division 10÷3, nous aurions quelque chose comme :

$divtofraction-010$

L'impossibiité d'obtenir un reste nul semble nous empêcher d'écrire les fractions "habituelles" : tout ce que nous pouvons tirer de ce genre d'opération est une valeur approchée du quotient, mais pasun quotient exact. Nous dirons par exemple que 10 ÷ 3 ≈ 3,33.

Pourtant, de cette division nous pouvons tirer une fraction !

Explication :

D'après la Partie 1, une fraction représente un partage "absolu" sans reste, autrement dit un partage "parfait". Dans la division 10÷3 nous pouvons "imaginer"quece partage parfait existe, même si nous ne sommes pas capables de le calculer !

Par conséquent, nous pourrons dire que :

La fraction $divtofraction-011$ représente le quotient exact de la division 10÷3 ,

et une valeur approchée de ce quotient est 3,333 .

Bilan

A part le vocabulaire qu'il faut connaître, vous devez savoir :

Que n'importe quelle division avec reste nul peut être écrite sous la forme de deux fractions.

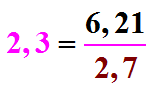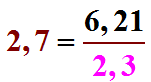(Exemple : 6,21 ÷ 2,3 = 2,7 donnera $divtofraction-008$ ou bien $divtofraction-009$ )

Que toute division "qui ne tombe pas juste" peut être écrite sous la forme d'une fraction.

(Exemple : 10 ÷ 3 ≈ 3,33 pourra quand même s'écrire $divtofraction-011$ )

| Mention légale |