Diviseurs et Multiples
Dans cette section, nous allons voir la définition du "diviseur d'un nombre" ainsi que celle du "multiple d'un nombre" avec quelques exemples simples.
Cette section fait suite aux différentes sections sur la divisions. Il est donc recommandé de maîtriser les tables de multiplications, la division par 9, la division par 11, ainsi que la division traditionnelle avec diviseurs à un ou deux chiffres.
1ère partie - Ce que nous enseignent les tables de multiplications
Les tables de multiplications sont toutes basées sur le même modèle.
Par exemple, nous savons que 15 = 5 x 3 = 3 x 5 .
La connaissance de ces schémas permet non seulement de trouver combien font 5 x 3 ou 3 x 5, mais en plus elle nous indique que 15 est à la fois dans la table de 3 et dans celle de 5 .
Plutôt que d'écrire (ou dire) que "15 est dans la table de multiplication de 5 et de 3" , nous écrivons (ou disons) :
"15 est un multiple de 5 et de 3 "
ou bien
"15 est divisible par 5 et par 3 " .
(Cette formulation a le mérite d'être plus courte que la première.)
A l'inverse, si nous savons que 15 = 5 x 3 = 3 x 5, nous savons aussi que 15 divisé par 5 donne 3 (avec un reste 0), et que 15 divisé par 3 donne 5 (avec un reste 0).
Au lieu d'écrire (ou dire) la phrase précédente, nous écrivons (ou disons) :
5 est un diviseur de 15, ou bien 3 est un diviseur de 15 .
(le reste qui vaut 0 est sous-entendu dans l'expression "est un diviseur de ")
De la même manière, puisque 21 = 7 x 3 , nous pouvons dire que 21 est un multiple de7 (et de3) et que 7 (ou 3) sont des diviseurs de 21.
On peut même aller plus loin : Si 1 x 2 x 3 x 5 = 30, cela veut dire que 1, 2, 3 et 5 sont les diviseurs de 30 , et que 30 est un multiple de 1, 2, 3 et 5.
Application
Répondre aux questions suivantes avec les expressions "un diviseur" ou "un multiple" au singulier ou au pluriel (passer votre souris sur les pointillés pour vérifier votre réponse) :
- Si 36 = 4 x 9 , alors 36 est ... de 4 .
- Si 72 = 8 x 9 alors 9 est ... de 72 .
- Puisque 12 = 4 x 3 et que 12 = 2 x 6, alors 4 , 3 , 2 et 6 sont ... de 12 .
- Puisque 15 = 5 x 3 et 25 = 5 x 5, alors 15 et 25 sont ... de 5.
- Puisque 12 = 1 x 12 = 2 x 6 = 3 x 4 , alors 1, 2, 3, 4, 6 et 12 sont ... de 12.
2ème partie - Le 1, un diviseur pas comme les autres
Nous avons tous appris que :
0 x 1 = 0 ; 1 x 1 = 1 ; 2 x 1 = 2 ; 3 x 1 = 3 ; etc.
Il en va d'ailleurs de même avec n'importe quel nombre entier ou décimal.
On pourrait résumer cette propriété en écrivant que si "a" désigne n'importe quel nombre entier ou décimal, on aura toujours :
a x 1 = a
En vertu de la Partie 1, nous pouvons donc dire deux choses :
- 1 est le diviseur de tous les nombre,
- et n'importe quel nombre "a" est son propre multiple et son propre diviseur.
Autrement dit :
- N'importe quelle division où le diviseur est 1 donnera toujours un reste de 0,
- et si on divise un nombre par lui-même, on aura toujours un reste égale à 0.
(N.B. : Si on est amené à chercher tous les diviseurs d'un nombre, il faudra penser à 1 et au nombre lui-même !)
Application
Répondre aux questions suivantes (passer votre souris sur les pointillés pour vérifier votre réponse) :
- Tous les diviseurs de 24 sont ...
- Les diviseurs communs à 15 et 21 sont ...
- Le nombre dont les diviseurs sont 1, 2, 3 et 7 est ...
- Les nombres pairs (0, 2, 4, 6, etc.) sont tous des multiples de ...
- Les deux uniquesdiviseurs de 7 sont ...
3ème partie - Les nombres premiers
Dans l'application précédente, nous avons rencontré un nombre qui ne possède que deux diviseurs : le 7 .
Le 7 fait partie d'une grande famille (infinie) qui regroupe tous les nombres qui ne possèdent que deux diviseurs : 1 et eux-mêmes. Ils sont appelés les nombres premiers.
Le mathématicien Euclide a prouvé, vers 300 av J.C. que cette grande famille était infinie. Autrement dit, il existe toujours un nombre premier plus grand que celui qu'on vient de trouver.
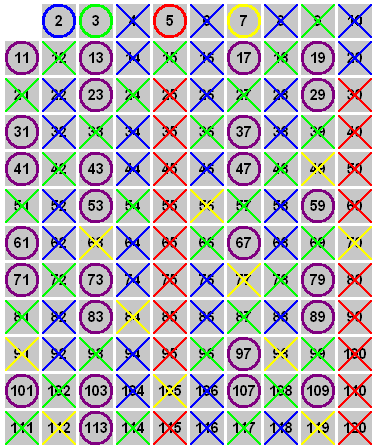
Pour les curieux, voici un lien qui explique comment trouver les nombres premiers inférieurs à 120 (entourés en violet sur la figure suivante) :